Problemas de Álgebra vectorial
Dados los vectores 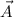 y
y  con origen en el punto común
con origen en el punto común 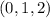 y extremos A(-1,2,3) y B(2,-1,1) respectivamente, calcular:
y extremos A(-1,2,3) y B(2,-1,1) respectivamente, calcular:
1.Producto escalar  .
.
2.Producto vectorial 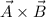 .
.
3.Producto vectorial 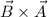 .
.
La velocidad de un móvil es 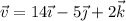 . Una fuerza
. Una fuerza 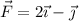 actúa sobre él. Calcula la componente de dicha fuerza en la dirección del movimiento y en la dirección perpendicular a él.
actúa sobre él. Calcula la componente de dicha fuerza en la dirección del movimiento y en la dirección perpendicular a él.
Nota previa: se sobreentiende que las cantidades que aparecen en el enunciado corresponden al sistema internacional de unidades.
Para determinar la componente de la fuerza en la dirección del movimiento (o componente tangencial, debido a que la velocidad posee ese carácter de ser tangente a la trayectoria), podemos comenzar determinando la proyección de la fuerza sobre velocidad, 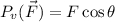 , siendo
, siendo  el ángulo que forman la fuerza y la velocidad. Recordando que el producto escalar de dos vectores se define como
el ángulo que forman la fuerza y la velocidad. Recordando que el producto escalar de dos vectores se define como 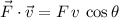 , tenemos que
, tenemos que
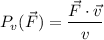
Como 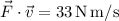 y
y 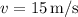 , tenemos que
, tenemos que 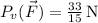 .
.
Para transformar esta cantidad escalar en un vector que lleve la dirección de la velocidad bastará con multiplicarla por un vector unitario que tenga la misma dirección y sentido que esta última, es decir,
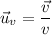
que en nuestro caso será 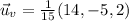 .
.
En consecuencia, la componente tangencial de la fuerza será 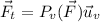 , que en este ejercicio valdrá
, que en este ejercicio valdrá 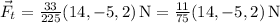 .
.
Observemos que usando (1) y (2) podemos escribir para la componente tangencial la expresión general
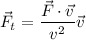
Una vez que conocemos la componente tangencial, encontrar la perpendicular (o normal), que denotaremos por 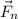 , es muy fácil puesto que
, es muy fácil puesto que 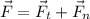 . En definitiva,
. En definitiva,
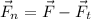
Substituyendo los valores del ejercicio, encontramos que 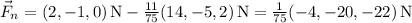 .
.
Dados los vectores 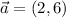 y
y 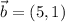 , calcula:
, calcula:
1.El producto escalar de ambos vectores.
2.La proyección de 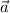 , sobre
, sobre 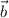
3.Las coordenadas de un vector unitario de la misma dirección que 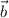
4.Un vector de la misma dirección que 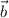 y cuyo módulo sea igual a la proyección de
y cuyo módulo sea igual a la proyección de 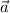 sobre
sobre 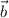 .
.
Dados dos vectores 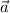 y
y 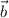 , obtener el vector proyección ortogonal de
, obtener el vector proyección ortogonal de 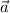 sobre
sobre 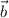 . Aplicarlo al caso en que [ERROR DE LaTeX. Error: 4 ] , [ERROR DE LaTeX. Error: 4 ] y
. Aplicarlo al caso en que [ERROR DE LaTeX. Error: 4 ] , [ERROR DE LaTeX. Error: 4 ] y 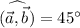 , obtener también la proyección ortogonal de
, obtener también la proyección ortogonal de 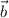 sobre
sobre 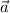 .
.
Halla el momento con respecto al punto P(0,-1,1) del vector unitario con origen en O(2,2,2) y que es paralelo al vector 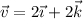 .
.


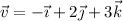 , halla otra de la misma dirección y sentido contrario, de módulo 3.
, halla otra de la misma dirección y sentido contrario, de módulo 3.