Problemas de movimiento lineal (1d)
Desde un Balcón situado a 14,1 m sobre el suelo de una calle, lanzamos un cuerpo verticalmente hacia arriba con una velocidad de 10 m/s. Calcular el tiempo que tardará en llegar al suelo.
En una carrera contrareloj, un ciclista recorre los primeros 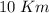 a una velocidad constante de
a una velocidad constante de 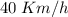 y los siguientes
y los siguientes 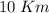 a una velocidad constante de
a una velocidad constante de 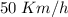 . ¿Cuál ha sido, globalmente, su velocidad media?
. ¿Cuál ha sido, globalmente, su velocidad media?
Una piedra cae desde un globo que desciende a una velocidad uniforme de 12m/s . Calcular la velocidad y la distancia recorrida por la piedra después de 10s. Resolver el mismo problema para el caso cuando el globo se eleva a la misma velocidad.
Desde un mismo punto se lanzan verticalmente hacia arriba, con un intervalo de 2s, dos objetos A y B con velocidades respectivas de 50m/s y 80m/s. Calcula el tiempo que tardan en encontrarse, la altura a la que lo hacen y la velocidad de cada uno cuando se encuentran.
Un globo está ascendiendo a razón de 12 m/s hasta una altura de 80 m, momento en el que suelta un paquete. ¿Cuánto tardará en llegar al suelo?
Lanzamos un objeto hacia arriba con una velocidad inicial de 100m/s. En ese mismo instante, dejamos caer, sin velocidad inicial, un segundo objeto que se encuentra inicialmente a 200m de altura.
1.¿A qué altura del suelo se cruzan?
2.¿Qué velocidad posee cada objeto en ese instante?
3.¿En qué sentido se mueve cada uno?
Para conocer el punto en que se cruzan necesitamos las ecuaciones de movimiento de ambos móviles, como se mueven en dirección paralela a la vertical, es decir el eje 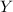 , podemos considerar la ecuación de movimiento como
, podemos considerar la ecuación de movimiento como 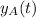 e
e 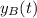 respectivamente.
respectivamente.
Para el cuerpo 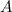 , el que lanzamos hacia arriba, la ecuación toma la forma
, el que lanzamos hacia arriba, la ecuación toma la forma 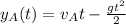 y para el cuerpo que dejamos caer,
y para el cuerpo que dejamos caer, 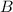 , será
, será 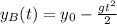 . Obviamente cuando se cruzan en
. Obviamente cuando se cruzan en 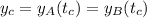 , igualando las dos expresiones
, igualando las dos expresiones
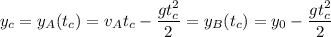
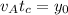
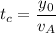
Si volvemos a la ecuación de 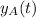 , o a
, o a 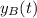
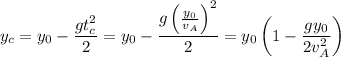
Con los datos que nos da el problema
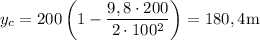
Para calcular la velocidad lo haremos a partir de las ecuaciones de movimiento, 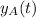 e
e 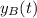 , sabiendo que
, sabiendo que 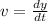 .
.
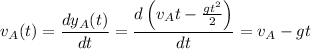
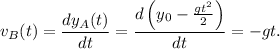
El tiempo 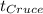 , lo conocemos del apartado anterior
, lo conocemos del apartado anterior 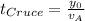 , así tenemos que:
, así tenemos que:
Si las escribimos en forma vectorial quedarían como:
Un cuerpo se deja caer libremente desde una altura de 800m. Simultáneamente un segundo cuerpo se dispara verticalmente desde el suelo con una velocidad inicial de 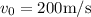 .
Calcular:
.
Calcular:
1.Tiempo que tardan en cruzarse.
2.A qué distancia del suelo se cruzan.
Desde un punto situado a una altura h, se lanza verticalmente una piedra hacia arriba con una velocidad de 29,4 m/s. Desde el mismo punto se deja caer otra piedra, 4 s después de lanzar la primera. Calcula:
1.¿En qué instante y en qué lugar alcanza la primera piedra a la segunda?
2.¿Qué velocidad tiene cada una de ellas en ese instante?
Una pelota se deja caer desde la ventana de un rascacielos y 2s después otra pelota se arroja verticalmente hacia abajo. ¿Cual debe ser la velocidad inicial de la segunda pelota si debe alcanzar a la primera en el instante exacto en que llega al suelo que esta a 400m bajo la ventana ?
La cabina de un ascensor, en la cual la distancia desde el suelo hasta el techo es igual a  , comienza a elevarse con aceleración constante de
, comienza a elevarse con aceleración constante de  después de dos segundos de iniciado el ascenso, comienza a caer un tornillo desde el techo del ascensor. Hallar
después de dos segundos de iniciado el ascenso, comienza a caer un tornillo desde el techo del ascensor. Hallar
1.el tiempo de caída libre del tornillo;
2.el desplazamiento y el espacio recorrido por el tornillo durante la caída libre en el sistema de referencia, relacionado con el ascensor.


