Problemas de integrales múltiples
Nivel: Primer ciclo
2
Bola con agujero cilíndrico
Nivel
Primer ciclo
Dificultad
7
3
Integral doble impropia
Nivel
Primer ciclo
Dificultad
8
Solución disponible
Metaleer
Empezaremos haciendo un cambio de variable,
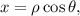
(1)
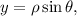
(2)
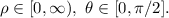
(3)
De esta manera, la integral queda (recordando que el teorema del cambio de variable exige multiplicar por el valor absoluto del jacobiano, 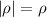 , ya que
, ya que 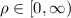 )
)
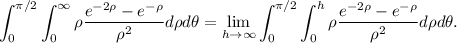
(4)
La discontinuidad del integrando en 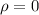 (límite inferior) es evitable, luego se puede simplificar el integrando para tener
(límite inferior) es evitable, luego se puede simplificar el integrando para tener
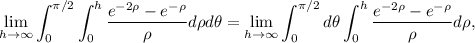
(5)
es decir
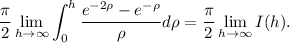
(6)
Teniendo en cuenta ahora que
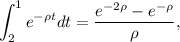
(7)
podemos expresar nuestra integral como
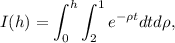
(8)
que, en virtud del teorema de Fubini, también es
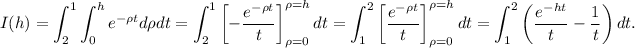
(9)
La última expresión no posee primitiva en términos de funciones elementales, pero recordemos que debemos tomar el límite cuando  tiende a
tiende a 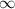 :
:
[ERROR DE LaTeX. Error: 5 : 656x43]
(10)
donde se puede demostrar que intercambiar el límite con el signo integral es una operación válida, por el Teorema de Convergencia Dominada.
Tenemos por tanto
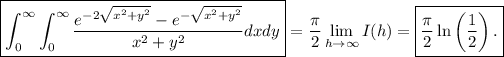
(11)

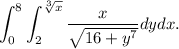

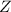 , de radio
, de radio 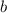 , que atraviesa de polo a polo la bola de radio
, que atraviesa de polo a polo la bola de radio  (con
(con 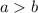 ) centrada en el origen. Calcule el volumen de la región así formada y, también, el área de su superficie.
) centrada en el origen. Calcule el volumen de la región así formada y, también, el área de su superficie.