Problemas de gravitación universal
Nivel: Primer ciclo
Supongamos un planetoide esférico y uniforme de masa 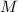 y radio
y radio 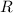 en el cual se ha realizado un pequeño túnel diametral que pasa por el centro. Demuestra que el movimiento de una partícula puntual en el interior de ese túnel es el de un oscilador armónico y halla su período. Considerar que el cuerpo nunca llega a salir del planetoide por las bocas del túnel.
en el cual se ha realizado un pequeño túnel diametral que pasa por el centro. Demuestra que el movimiento de una partícula puntual en el interior de ese túnel es el de un oscilador armónico y halla su período. Considerar que el cuerpo nunca llega a salir del planetoide por las bocas del túnel.
La teoría de la relatividad General predice pequeñas correcciones de la ley de la gravitación universal de Newton. Para un planeta de masa 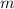 viajando a una velocidad
viajando a una velocidad  en una órbita de radio
en una órbita de radio  , la expresión para la fuerza modificada se puede escribir como
, la expresión para la fuerza modificada se puede escribir como
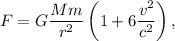
donde  es la velocidad de la luz y
es la velocidad de la luz y 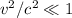 .
.
1.Encontrar que el periodo se puede escribir
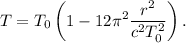
2.Mostrar que en cada revolución el planeta avanza un ángulo respecto al caso Newtoniano
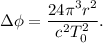
3.Aplicar estos resultados a Mercurio y verificar que el avance acumulado de la órbita después de un siglo es de cerca de 43'' de arco. Para el planeta Mercurio:  (donde ua = unidad astronómica = radio de la órbita terrestre).
(donde ua = unidad astronómica = radio de la órbita terrestre).


