Problemas de gravitación universal
Nivel: Primer ciclo
Supongamos un planetoide esférico y uniforme de masa 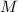 y radio
y radio 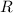 en el cual se ha realizado un pequeño túnel diametral que pasa por el centro. Demuestra que el movimiento de una partícula puntual en el interior de ese túnel es el de un oscilador armónico y halla su período. Considerar que el cuerpo nunca llega a salir del planetoide por las bocas del túnel.
en el cual se ha realizado un pequeño túnel diametral que pasa por el centro. Demuestra que el movimiento de una partícula puntual en el interior de ese túnel es el de un oscilador armónico y halla su período. Considerar que el cuerpo nunca llega a salir del planetoide por las bocas del túnel.
Para realizar este ejercicio, en primer lugar hemos de determinar el campo gravitatorio en el interior de cualquier punto del túnel. Al ser un túnel muy pequeño, podemos suponer que el campo será el mismo que existiría si no se hubiera realizado la perforación. Para realizar el cálculo, utilizamos la ley integral de Gauss para el campo gravitatorio,
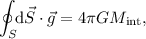
donde 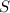 es una superficie cerrada, y
es una superficie cerrada, y  la masa que dicha esfera encierra. Dada la simetría esférica del sistema, la mejor elección posible para
la masa que dicha esfera encierra. Dada la simetría esférica del sistema, la mejor elección posible para 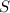 es una superficie esférica de radio
es una superficie esférica de radio  , siendo
, siendo  la distancia a la cual se encuentra el sistema. Sobre ésta superficie, el campo gravitatorio es constante y radial, por simetría, y se puede sacar de la integral. Por lo tanto, nos queda tan sólo la integración del elemento de superficie, que tiene la misma dirección que el campo y por lo tanto no obtenemos componente angular, que como resultado final nos da el área total de la esfera,
la distancia a la cual se encuentra el sistema. Sobre ésta superficie, el campo gravitatorio es constante y radial, por simetría, y se puede sacar de la integral. Por lo tanto, nos queda tan sólo la integración del elemento de superficie, que tiene la misma dirección que el campo y por lo tanto no obtenemos componente angular, que como resultado final nos da el área total de la esfera,
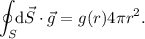
Por otra parte, dado que el planetoide es uniforme, su densidad será constante y la masa contenida en la esfera de radio  crecerá de forma proporcional al su volumen, es decir, al cubo del radio
crecerá de forma proporcional al su volumen, es decir, al cubo del radio

Por tanto, la ecuación (1) queda de la forma,

que, simplificando y dando el carácter vectorial en dirección radial, se escribe de la forma
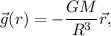
es decir, el campo gravitatorio es proporcional a la distancia al centro de fuerzas y, por lo tanto, la fuerza también lo es,

donde 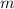 es la masa de la partícula que se mueve por el túnel. Ésta no es mas que la fuerza característica de un oscilador harmónico,
es la masa de la partícula que se mueve por el túnel. Ésta no es mas que la fuerza característica de un oscilador harmónico,  , donde podemos identificar
, donde podemos identificar

De la teoría general, sabemos que el período de un oscilador armónico es

por tanto, según la identificación de la ecuación (7) tenemos
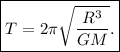
La teoría de la relatividad General predice pequeñas correcciones de la ley de la gravitación universal de Newton. Para un planeta de masa 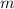 viajando a una velocidad
viajando a una velocidad  en una órbita de radio
en una órbita de radio  , la expresión para la fuerza modificada se puede escribir como
, la expresión para la fuerza modificada se puede escribir como
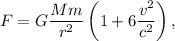
donde  es la velocidad de la luz y
es la velocidad de la luz y 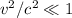 .
.
1.Encontrar que el periodo se puede escribir
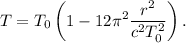
2.Mostrar que en cada revolución el planeta avanza un ángulo respecto al caso Newtoniano
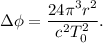
3.Aplicar estos resultados a Mercurio y verificar que el avance acumulado de la órbita después de un siglo es de cerca de 43'' de arco. Para el planeta Mercurio:  (donde ua = unidad astronómica = radio de la órbita terrestre).
(donde ua = unidad astronómica = radio de la órbita terrestre).


