Problemas de geometría lineal y espacio afín
Dados los planos
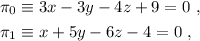
hallar la ecuación de la recta 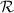 que pasa por el punto
que pasa por el punto 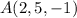 y es paralela a los dos planos.
y es paralela a los dos planos.
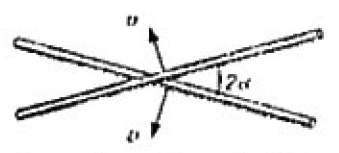
Dos barras se cruzan bajo un ángulo 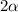 y se mueven con iguales velocidades
y se mueven con iguales velocidades  y perpendicularmente a si mismas, tal como se indica en la figura. ¿Cuál será la velocidad del punto de cruce de las barras?
y perpendicularmente a si mismas, tal como se indica en la figura. ¿Cuál será la velocidad del punto de cruce de las barras?
Una forma de resolución totalmente geométrica. Sabemos que en dos dimensiones una recta se puede escribir como
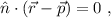
donde 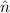 es un vector perpendicular a ella y
es un vector perpendicular a ella y 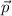 es un punto cualquiera de la recta. Este punto se moverá en la dirección perpendicular,
es un punto cualquiera de la recta. Este punto se moverá en la dirección perpendicular, 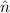 a la velocidad v.
a la velocidad v.
Elijo el eje OX de forma que pasa por la bisectriz de las dos varas. Para la bara superior, tenemos
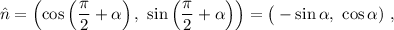
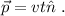
Por lo tanto, la ecuación que nos da la recta ocupada por esta primera barra será, teniendo en cuenta que 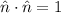 , es
, es
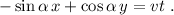
Para la segunda barra, está claro que hay que cambiar el valor de la coordenada y del vector perpendicular,
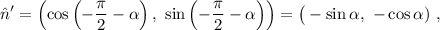
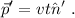
Y las mismas consideraciones nos llevan a la ecuación
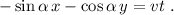
El punto de intersección de las barras será aquél que cumpla simultáneamente ambas ecuaciones. Restando (4) y (7) vemos que 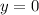 . Sumándolas
. Sumándolas
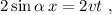
de donde
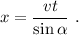
Por lo tanto, la velocidad de la intersección será
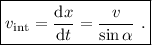

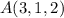 y es perpendicular a la recta
y es perpendicular a la recta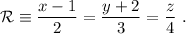

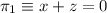 y
y 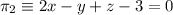 .
.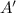 , del punto
, del punto 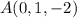 respecto del plano
respecto del plano 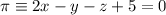 .
.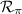 , proyección de la recta
, proyección de la recta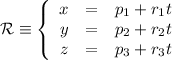
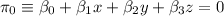 .
.