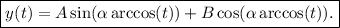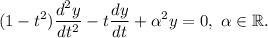Problemas de ecuaciones diferenciales ordinarias
Nivel: Primer ciclo
Encontrar la solución general de las siguientes ecuaciones diferenciales.
1.
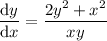
2.

3.
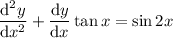
4.

Para resolver la ecuación diferencial
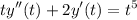
1.Obtenga la solución general de la ecuación diferencial homogénea asociada.
2.Demuestre la identidad
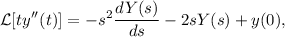
donde  representa la transformada de Laplace.
representa la transformada de Laplace.
3.Aplique transformadas de Laplace a la ecuación diferencial original y obtenga, de este modo, una solución particular.
4.Finalice mostrando la solución general obtenida.
Esta ecuación diferencial se puede resolver con la ayuda de los desarrollos en serie de Frobenius (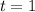 y
y 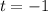 son puntos singulares regulares). No obstante, la vamos a resolver de una forma más elegante, haciendo el cambio de variable
son puntos singulares regulares). No obstante, la vamos a resolver de una forma más elegante, haciendo el cambio de variable 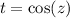 . Por la regla de la cadena
. Por la regla de la cadena
Observamos que hemos deducido la siguiente relación entre los operadores diferenciales:
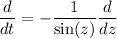
que usaremos para expresar la segunda derivada en términos de la nueva variable independiente  .
.
Sustituyendo en la ecuación diferencial, tenemos
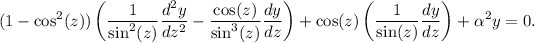
Recordando que 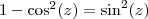
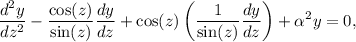
es decir
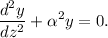
Esta ecuación diferencial ordinaria lineal de coeficientes constantes homogénea y de segundo orden se puede integrar fácilmente. El polinomio característico es  , con lo que debemos resolver la ecuación polinómica
, con lo que debemos resolver la ecuación polinómica
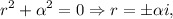
por lo que
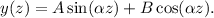
Deshaciendo el cambio de variable, obtenemos la solución buscada