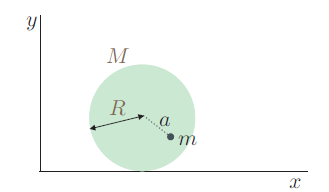
Un disco uniforme de masa 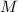 y radio
y radio 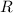 lleva adherida una masa
lleva adherida una masa 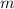 a una distancia a de su centro. Si el disco puede rodar sin deslizar sobre un plano horizontal, determine la frecuencia de las pequeñas oscilaciones alrededor de la posición de equilibrio. El plano que contiene al disco es vertical.
a una distancia a de su centro. Si el disco puede rodar sin deslizar sobre un plano horizontal, determine la frecuencia de las pequeñas oscilaciones alrededor de la posición de equilibrio. El plano que contiene al disco es vertical.
Encontraremos primero las ecuaciones de movimiento con la formulación de Lagrange para luego imponer en ellas las condiciones de pequeñas oscilaciones y que éstas sean alrededor de la posición de equilibrio.
 Coordenadas y velocidad de
Coordenadas y velocidad de 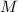 :
:
Debido a la ligadura de rodar sin deslizar 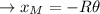 , donde el menos proviene de suponer que la apartamos del equilibrio hacia la izquierda tal que la masa
, donde el menos proviene de suponer que la apartamos del equilibrio hacia la izquierda tal que la masa 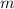 quede a la derecha de la vertical que pasa por el radio para concordar con la figura.
Así:
quede a la derecha de la vertical que pasa por el radio para concordar con la figura.
Así:
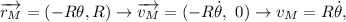
lo que era de esperar por la condición de rodadura, donde 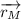 es la posición del CM del disco de masa
es la posición del CM del disco de masa 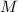 .
.
 Coordenadas y velocidad de
Coordenadas y velocidad de 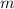 :
:
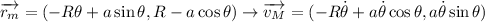
con lo que
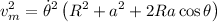
Para las energías cinéticas:

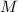 tendrá energía cinética de traslación y de rotación. Si suponemos que es rígido:
tendrá energía cinética de traslación y de rotación. Si suponemos que es rígido:
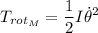
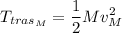
Calculemos el momento de inercia del disco: El tensor de inercia para una distribución continua de masa es:
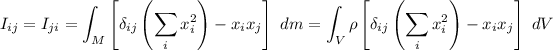
Como nos interesa el momento principal de inercia 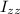 que se corresponde al momento de inercia respecto a un eje perpendicular al disco que pase por su centro, nos queda la integral (si además consideramos que es una distribución continua superficial de masa cuya densidad superficial es constante):
que se corresponde al momento de inercia respecto a un eje perpendicular al disco que pase por su centro, nos queda la integral (si además consideramos que es una distribución continua superficial de masa cuya densidad superficial es constante):
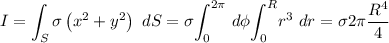
donde hemos hecho un cambio a coordenadas cilíndricas.
Si tenemos en cuenta que 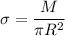 de la definición de densidad superficial, queda:
de la definición de densidad superficial, queda:
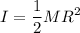
luego
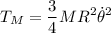

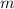 tendrá energía cinética de traslación únicamente dada por
tendrá energía cinética de traslación únicamente dada por
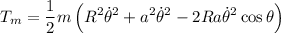
Con lo que
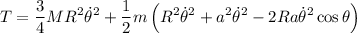
La energía potencial será
 Para
Para 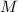 :
:
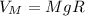
 Para
Para 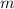 :
:
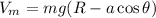
por lo que
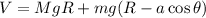
La Lagrangiana será:
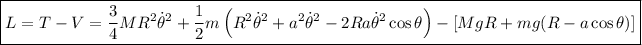
De las ecuaciones de Lagrange, para nuestra única coordenada generalizada  nos queda:
nos queda:

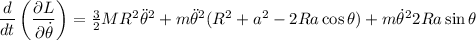

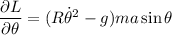
Con lo que
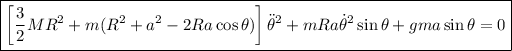
ahora imponemos
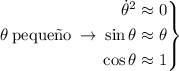
Luego nuestra ecuación de movimiento se reduce a
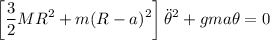
Lo cual es un M.A.S. de frecuencia angular:
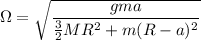
de donde como 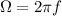 ;
;
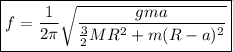
Como nota, vemos que si 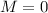 (soporte sin masa) y
(soporte sin masa) y 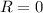 queda la frecuencia de un M.A.S. hecho por
queda la frecuencia de un M.A.S. hecho por 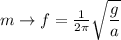 comportándose como un péndulo de pequeña amplitud.
comportándose como un péndulo de pequeña amplitud.