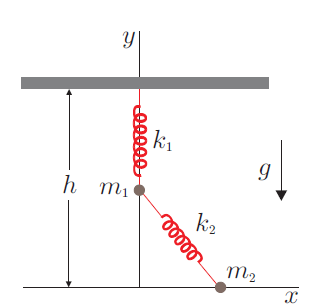
Considere el sistema de la figura, donde la masa 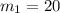 kg está obligada a moverse verticalmente según el eje y, mientras que m
kg está obligada a moverse verticalmente según el eje y, mientras que m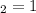 kg está obligada a moverse según el eje x, ambas bajo la acción de dos muelles de constantes recuperadoras
kg está obligada a moverse según el eje x, ambas bajo la acción de dos muelles de constantes recuperadoras 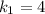 N/m y
N/m y 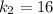 N/m, además de la gravedad (Considere la longitud en reposo de los muelles nula).
N/m, además de la gravedad (Considere la longitud en reposo de los muelles nula).
1.Calcule la lagrangiana del sistema.
2.Obtenga las ecuaciones del movimiento para las masas.
3.Obtenga la solución general de las mismas y la posición de equilibrio.
4.Escriba la solución sabiendo que inicialmente se parte del reposo con  m,
m,  m. Si
m. Si 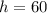 m y
m y 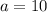 m, determine la posición de las masas al cabo de
m, determine la posición de las masas al cabo de 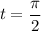 segundos.
segundos.
Colocamos el origen de coordenadas en el punto inferior central del diagrama (donde interseccionan las trayectorias posibles de cada masa).
 Para
Para 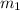 :
:
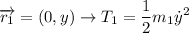
 Para
Para 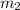 :
:
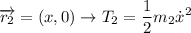
Luego para la energía cinética:
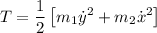
Si escogemos la recta 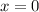 como origen para
como origen para  tendríamos que la energía potencial gravitatoria total del sistema sería:
tendríamos que la energía potencial gravitatoria total del sistema sería:
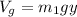
Para la energía potencial elástica almacenada en los muelles:
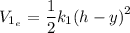
y
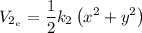
donde el alargamiento del segundo muelle sale del teorema de pitágoras.
La Lagrangiana será:
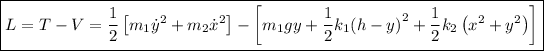
De las ecuaciones de Lagrange:
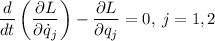
nos queda:
 Para
Para  :
:
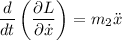
y
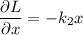
Luego
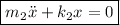
 Para
Para  :
:
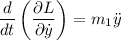
y
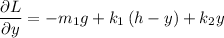
Luego
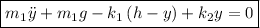
Tenemos el sistema:
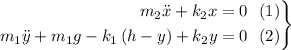
 Para (1):
Para (1):
Es una ecuación diferencial de segundo orden homogénea, cuyo polinomio característico es 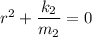 .
Definiendo
.
Definiendo 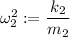 nos queda:
nos queda:
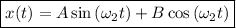
siendo 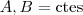 .
.
 Para (2):
Para (2):
Es una ecuación diferencial lineal de segundo orden (no homogénea pues posee término independiente). Definimos 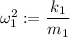 . Reorganizando:
. Reorganizando:
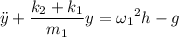
Resolvemos la parte homogénea:
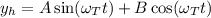
siendo 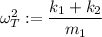
Para encontrar la solución particular, notamos en la ecuación (17) que tanto el término inohomogéneo como los coeficientes de la parte homogénea son constantes. Esto nos inspira la posibilidad de elegir una solución particular constante, 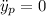 . Substituyendo, obtenemos
. Substituyendo, obtenemos
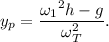
Por lo que 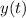 queda:
queda:
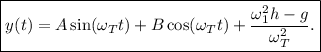
Si en las ecuaciones de movimiento hubiéramos impuesto la condición de equilibrio ( y
y 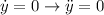 ) nos quedarían:
) nos quedarían:
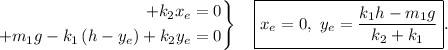
Las condiciones impuestas por el enunciado equivalen a
 Para
Para  :
:
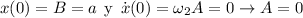
por lo que
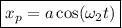
 Para
Para  :
:

por lo que

Si 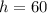 m y
m y 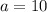 m, para
m, para 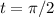 , como
, como 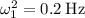 ,
,  y
y 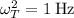 , con
, con 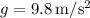 nos queda:
nos queda:
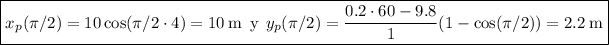
Como corolario, veamos con el formalismo de Newton que en el equilibrio la sumatoria de las fuerzas en el eje y para la masa 1 es nula. Con los datos 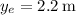 , luego está en la posición de equilibro, luego el peso de la masa uno más la componente sobre el eje y de la fuerza del muelle dos cuando la segunda masa está en
, luego está en la posición de equilibro, luego el peso de la masa uno más la componente sobre el eje y de la fuerza del muelle dos cuando la segunda masa está en 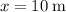 tiene que ser igual a la fuerza del muelle uno en dicha posición. En dicha posición la componente de la fuerza elástica del segundo muelle sobre el eje
tiene que ser igual a la fuerza del muelle uno en dicha posición. En dicha posición la componente de la fuerza elástica del segundo muelle sobre el eje  es
es 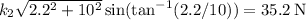 , el peso
, el peso 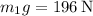 y la fuerza del muelle 1
y la fuerza del muelle 1 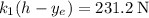 lo que vemos que coincide con la suma de las dos anteriores.
lo que vemos que coincide con la suma de las dos anteriores.