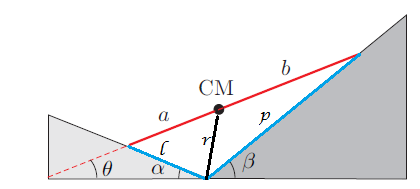
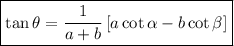Una varilla, cuyo centro de masa CM la divide en dos partes de longitudes  y
y 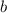 , se encuentra en equilibrio con sus extremos apoyados sobre dos planos inclinados de ángulos
, se encuentra en equilibrio con sus extremos apoyados sobre dos planos inclinados de ángulos 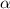 y
y 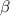 respecto de la horizontal. Mediante el método de los trabajos virtuales, determine el ángulo
respecto de la horizontal. Mediante el método de los trabajos virtuales, determine el ángulo  que la varilla forma con la horizontal en la posición de equilibro. El rozamiento es nulo.
que la varilla forma con la horizontal en la posición de equilibro. El rozamiento es nulo.
La única fuerza es el peso 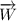 (y las dos normales en los extremos, pero debido a su perpendicularidad a los planos que los soportan, los desplazamientos de dichos puntos siempre seran perpendiculares a las normales, i.e. las normales no realizan trabajo).
(y las dos normales en los extremos, pero debido a su perpendicularidad a los planos que los soportan, los desplazamientos de dichos puntos siempre seran perpendiculares a las normales, i.e. las normales no realizan trabajo).
Si tomamos como origen el punto donde las cuñas se juntan, y ahí dos ejes cartesianos x e y, tendremos que:
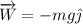
y del dibujo:
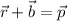
Con 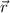 el vector posición del centro de masa y siendo:
el vector posición del centro de masa y siendo:
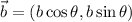
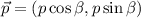
luego
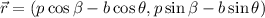
Si la barra desliza, lo que varían son 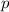 y
y  :
:
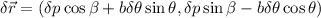
Asi, de
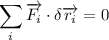
queda
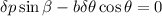
Necesitamos una relación del tipo 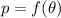 para poder dejar nuestra expresión solo en función de
para poder dejar nuestra expresión solo en función de  .
.
De la trigonometria vemos que si proyectamos el vector 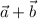 sobre el eje x y sobre el eje y:
sobre el eje x y sobre el eje y:
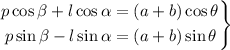
despejando  en la primera y substituyendo en la segunda queda:
en la primera y substituyendo en la segunda queda:
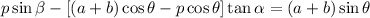
o lo que es lo mismo:
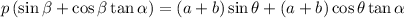
luego
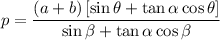
y ya diferenciando

si llamamos
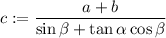
para simplificar, y ya sustituyendo 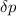 en
en 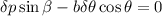 queda:
queda:
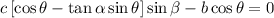
Reorganizando y dividiendo entre 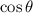 :
:
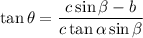
y como 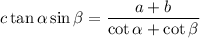 y
y 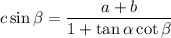 finalmente queda
finalmente queda