Imagina que la nave más rápida del hombre pudiese viajar a una velocidad de 0.866c. Así que la NASA planea un viaje a un planeta que se encuentra a 50 años luz de la tierra. Entonces el astronauta hace un cálculo rápido y contesta: ¡Los físicos estáis locos! Tardaré 115 años en ir y volver, como ahora tengo 20, ¡tendría que vivir hasta los 135! Pero en ese momento uno de los físicos del programa le corrige diciéndole que no se preocupe porque el viaje va a ser más corto de lo que piensa y que va ha llegar vivo (ten en cuenta una esperanza de vida de 85 años). El astronauta estupefacto pide al físico que le demuestre que va a sobrevivir.
La pregunta es, ¿Cuánto tiempo va a tardar en llegar la nave desde el punto de vista del astronauta, con v=0.866; distancia = 100 años luz? ¿Va ha sobrevivir? (Datos extra: 1 año luz = 9.33e15m)
Para resolver esta aparente paradoja o imposibilidad, no hace falta nada más que conocer la equación del intervalo en el espacio-tiempo. Podríamos resolverla mediante las transformaciones de lorentz pero sería más laborioso.
En realidad usando la invarianza del intervalo no hace falta cambiar de unidades, podemos operar con años luz para x y años para t. (Cuidado! esto solo es útil en este caso!)
Primero, el intervalo se define (en nuestro espacio bidimensional, x-t) cómo:
Observador en movimiento O' (en el cohete), en reposo O (en la tierra).
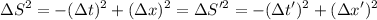
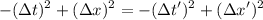
Si aislamos 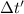 teniendo en cuenta que para el astronauta el intervalo va a tener un desplazamineto en x igual a zero, (
teniendo en cuenta que para el astronauta el intervalo va a tener un desplazamineto en x igual a zero, (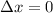 ) obtenemos que:
) obtenemos que:
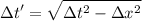
Substituimos...
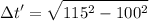
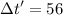
Así que para el astronauta sólo habrán pasado 56 años! Por lo tanto tendrá 76 y no 135 cómo pensaba! En cambio para el físico que se quedó en tierra habrán pasado 115 años...


