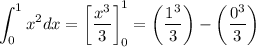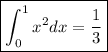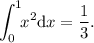La integración es la operación inversa de la derivación, así, la integral de una función f(x) es otra función y(x) tal que:
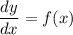 es decir:
es decir:
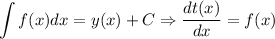
En este caso, nos encontramos ante una integral definida, es decir, una integral entre dos límites; a diferencia de las indefinidas, con infinitas soluciones, que se diferencian en el valor de la constante de integración C, las integrales definidas tienen una única solución, y esto es lo que queremos demostrar.
Haciendo uso de la definición, imaginemos que queremos calcular de la forma más precisa el área encerrada bajo la curva de una función que se encuentra entre los límites 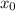 y
y  . El método a seguir sería dividir esa área en rectángulos y la suma de las áreas de los rectángulos nos daría la primera aproximación; la aproximación será más exacta si la base de dichos rectángulos
. El método a seguir sería dividir esa área en rectángulos y la suma de las áreas de los rectángulos nos daría la primera aproximación; la aproximación será más exacta si la base de dichos rectángulos 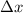 tiende a cero, luego:
tiende a cero, luego:
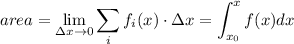
La integral definida es igual a la diferencia entre la solución de la integral en  (límite superior) y
(límite superior) y 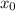 límite superior, que es lo que se conoce como regla de Barrow. Por tanto:
límite superior, que es lo que se conoce como regla de Barrow. Por tanto: