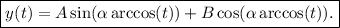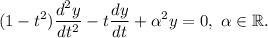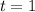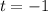Esta ecuación diferencial se puede resolver con la ayuda de los desarrollos en serie de Frobenius ( y son puntos singulares regulares). No obstante, la vamos a resolver de una forma más elegante, haciendo el cambio de variable 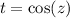. Por la regla de la cadena

Observamos que hemos deducido la siguiente relación entre los operadores diferenciales:

(2)

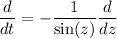
que usaremos para expresar la segunda derivada en términos de la nueva variable independiente .

Sustituyendo en la ecuación diferencial, tenemos

(4)

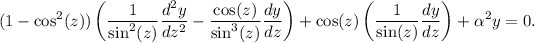
Recordando que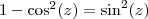

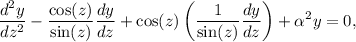
(5)

es decir

(6)

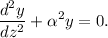
Esta ecuación diferencial ordinaria lineal de coeficientes constantes homogénea y de segundo orden se puede integrar fácilmente. El polinomio característico es , con lo que debemos resolver la ecuación polinómica

(7)

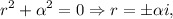
por lo que

(8)

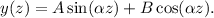
Deshaciendo el cambio de variable, obtenemos la solución buscada

(9)