Empezaremos por recordar el significado del productorio,
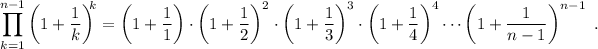
Paso 1. Debemos comprobar que la igualdad se cumple para el primer valor posible, que en este caso es 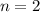 . En este caso, el productorio sólo tiene un factor,
. En este caso, el productorio sólo tiene un factor,
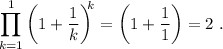
El lado derecho de la igualdad es
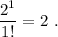
Por lo tanto, la igualdad se cumple para 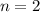 .
.
Paso 2. Por hipótesis, suponemos que la igualdad se cumple para n arbitrario,
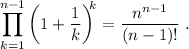
Paso 3. Utilizando (4), debemos demostrar que la igualdad también se cumple para 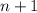 ,
,
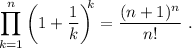
Comenzaremos desarrollando el productorio de (5),
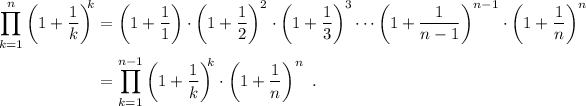
Excepto el último factor, el resto son idénticos a los de (4), por lo que podemos simplemente substituir,
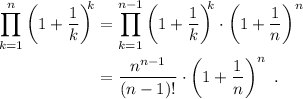
Para continuar, realizamos la suma de fracciones en el término entre paréntesis,
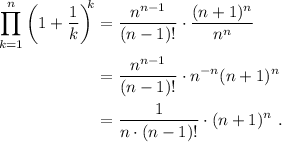
Utilizando la definición de factorial vemos que 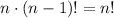 , por lo tanto
, por lo tanto
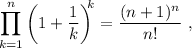
que coincide con el valor que esperábamos. Por lo tanto, (5) es cierto si (4) lo es. Esto completa la demostración por inducción.

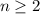 , se cumple
, se cumple
