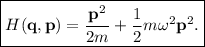Considera un oscilador armónico multidimensional, dado por el potencial
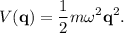
Encuentra el lagrangiano, los momentos conjugados y el hamiltoniano del sistema. Utiliza coordenadas rectilíneas.
En general, el lagrangiano de un sistema mecánico se escribe de la forma
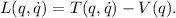
En coordenadas rectilíneas (cartesianas), la energía cinética viene dada simplemente por
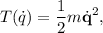
con lo que el lagrangiano es
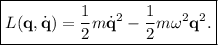
Los momentos conjugados se definen como la derivada respecto de 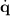 del lagrangiano,
del lagrangiano,
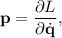
con lo cual, tenemos
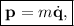
es decir, en este contexto, el momento conjugado coincide con la cantidad de movimiento, o momento lineal.
El hamiltoniano se define de la forma
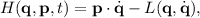
donde debemos expresarlo todo en función de los momentos solamente de los momentos, y no de las velocidades. El resultado final se obtiene fácilmente, y es