Encontrar la raíz cerca de 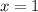 de
de 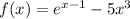 empezando con
empezando con 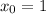 . ¿Cuán exacta es la estimación después de cuatro iteraciones del método de Newton? ¿Cuántas iteraciones requiere el método de la bisección para lograr la misma exactitud?. Tabule el número de dígitos correctos en cada iteracción del método de Newton y observe si se duplican cada vez. La solución correcta es x = 0.49404364.
. ¿Cuán exacta es la estimación después de cuatro iteraciones del método de Newton? ¿Cuántas iteraciones requiere el método de la bisección para lograr la misma exactitud?. Tabule el número de dígitos correctos en cada iteracción del método de Newton y observe si se duplican cada vez. La solución correcta es x = 0.49404364.
Para obtener una solución a 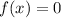 mediante el método de Newton, dada la función diferenciable
mediante el método de Newton, dada la función diferenciable 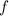 y una aproximación inicial
y una aproximación inicial 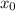 , utilizamos el siguiente algoritmo:
, utilizamos el siguiente algoritmo:
En nuestro caso, dada la aproximación inicial 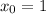 y las funciones
y las funciones 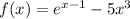 y
y 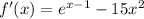 , para
, para 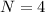 iteraciones, tenemos la siguiente tabla de los valores obtenidos:
iteraciones, tenemos la siguiente tabla de los valores obtenidos:
| N | 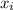 |
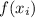 |
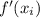 |
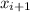 |
|---|---|---|---|---|
| 0 | 1.000000 | -4.000000 | -1.400000 | 0.714286 |
| 1 | 0.714286 | -1.070682 | -6.901590 | 0.559150 |
| 2 | 0.559150 | -0.230598 | 4.046242 | 0.502159 |
| 3 | 0.502159 | -0.025100 | -3.174613 | 0.494222 |
| 4 | 0.494222 | -0.000545 | -3.060792 | 0.494043 |
En este método iterativo debería cumplirse que el número de decimales de exactitud se duplica en cada iteración. Como podemos comprobar en la tabla, esto se cumple para 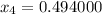 con tres decimales exactos, y
con tres decimales exactos, y 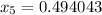 con seis decimales exactos. La tolerancia alcanzada mediante el método de Newton es de
con seis decimales exactos. La tolerancia alcanzada mediante el método de Newton es de 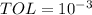 . Para saber cuántas iteraciones son necesarias para lograr dicha tolerancia mediante el método de la bisección, con el intervalo
. Para saber cuántas iteraciones son necesarias para lograr dicha tolerancia mediante el método de la bisección, con el intervalo 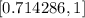 , hay que encontrar un número entero
, hay que encontrar un número entero 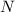 que satisfaga:
que satisfaga:
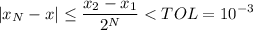
por tanto, tenemos
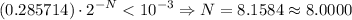
Vemos pues, que para el método de la bisección se necesitarían, aproximadamente, el doble de iteraciones que para el método de Newton.



