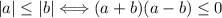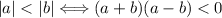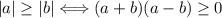La web de Física - Números Reales
Jorge A. Chávez S. - N30F3B0
1. Resumen
En estos apuntes se presentan a modo de formulario, la definición axiomática de los números reales así como algunas de sus propiedades y definiciones importantes.
2. Conjunto de los números reales
Definición 1 (Axiomas de los números reales)
El conjunto de los números reales 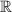 es un cuerpo ordenado y completo provisto de dos operaciones
es un cuerpo ordenado y completo provisto de dos operaciones  (suma) y
(suma) y  (multiplicación) donde existen dos elementos
(multiplicación) donde existen dos elementos 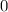 y
y  , así como un conjunto
, así como un conjunto  tal que:
tal que:
1. 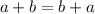 y
y 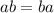
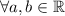
2. 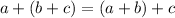 y
y 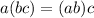
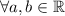
3. 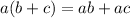
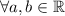
4. 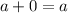 y
y 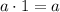
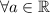
5.
Para cada 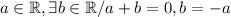
Para cada 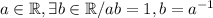
6. Dados 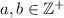 entonces si
entonces si 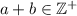 ;
; 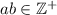 . Los elementos de
. Los elementos de 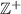 son llamados positivos.
son llamados positivos.
7. Dado 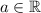 , se cumple solo una de las siguientes posibilidades
, se cumple solo una de las siguientes posibilidades 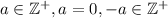
Definición 2 (Relación de orden)
Se define 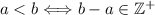
8. Sea 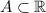 , un subconjunto no vacío y que existe un
, un subconjunto no vacío y que existe un 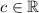 tal que
tal que 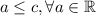 . Entonces existe un número mayor a cualquier elemento de
. Entonces existe un número mayor a cualquier elemento de 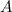 tal que es menor o igual que cualquier otro número mayor a cualquier elemento de
tal que es menor o igual que cualquier otro número mayor a cualquier elemento de 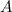
Definición 3 (Resta)
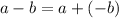
Definición 4 (División)
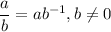
3. Algunas propiedades importantes
Sean 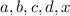 números reales
números reales
1. 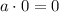
2. 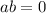 si y solo si
si y solo si 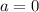 ó
ó 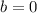
3. 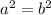 si y solo si
si y solo si 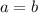 ó
ó 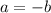
4. Si 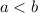 y
y 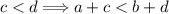
5. Si 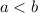 y
y 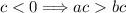
6. Si 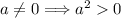
7.
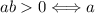 y
y 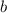 tienen el mismo signo.
tienen el mismo signo.
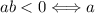 y
y 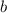 tienen signos opuestos
tienen signos opuestos
8. Si  y
y 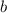 tienen el mismo signo y
tienen el mismo signo y 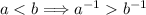
9. Si 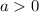 y
y 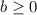 entonces
entonces 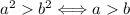
10. Dado 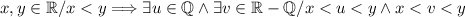
11. Dados 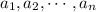 y
y  y
y 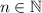 se cumple
se cumple
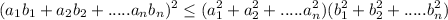
Definición 5 (Raíz de un número positivo)
Sea  ,
,  . Definimos
. Definimos ![\sqrt[n]{a} \sqrt[n]{a}](/latexrender/pictures/11_bf7ff33f3b129b15c06203d60f007807.png) como siendo el único número real positivo tal que:
como siendo el único número real positivo tal que:
![\displaystyle \dst(\sqrt[n]a)^n=a \displaystyle \dst(\sqrt[n]a)^n=a](/latexrender/pictures/33_4e6904e22ad3e95944679712173112ea.png)
Si 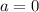 definimos
definimos ![\sqrt[n]{a}=0 \sqrt[n]{a}=0](/latexrender/pictures/13_ee5b91b35285880ab4d5ad91acb7938d.png)
12. Si 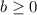 entonces
entonces 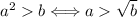 ó
ó 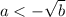
13. Si 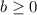 entonces
entonces 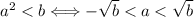
14. Dados  y
y 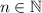 se cumple que:
se cumple que:
![\displaystyle \dst\sqrt[n]{x_1x_2...x_n} \leq \frac{x_1+x_2+.......x_n}{n} \displaystyle \dst\sqrt[n]{x_1x_2...x_n} \leq \frac{x_1+x_2+.......x_n}{n}](/latexrender/pictures/74_ee47c37e73bf26fde4a343b6ab6db7d1.png)
Definición 6 (Valor absoluto)
El valor absoluto de un número real se denota por 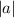 y se define así:
y se define así:
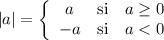
15. 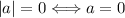
16. 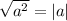 , para todo
, para todo 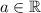
17. 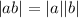
18. Desigualdad Triangular
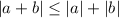
19. ![|a|=b \Longleftrightarrow b\geq0\wedge [a=b\vee a=-b] |a|=b \Longleftrightarrow b\geq0\wedge [a=b\vee a=-b]](/latexrender/pictures/53_2811fcce7668da22d79953d2f4cf3579.png)
20. 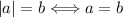 o
o 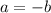
21.
![|x|\leq a\Longleftrightarrow[a\geq0\wedge -a\leq x\leq a] |x|\leq a\Longleftrightarrow[a\geq0\wedge -a\leq x\leq a]](/latexrender/pictures/57_fced28f4a4223e0dbeece703d4f1b036.png)
![|x|< a\Longleftrightarrow[a<0\wedge -a< x< a] |x|< a\Longleftrightarrow[a<0\wedge -a< x< a]](/latexrender/pictures/45_6d4cd5b5fffd6b6a90f74c117a9873c2.png)
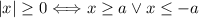
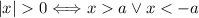
22.